矩阵模和矩阵模板是数学和计算机科学中的两个概念,它们在各自的领域中有特定的应用。
1、矩阵模:
定义矩阵模通常指的是矩阵的某种范数(norm),它是一种衡量矩阵大小或长度的数学工具,不同的范数定义可以反映矩阵的不同特性,如列空间的几何性质、行空间的几何性质等,常见的矩阵范数包括L1范数、L2范数(也称为欧几里得范数或谱范数)等,这些范数的具体定义和应用场景因上下文而异。
应用领域矩阵的范数在计算机图形学、线性代数、数值分析等学科中有广泛的应用,特别是在解决线性方程组、优化问题等方面,在机器学习领域,矩阵的范数也常用于优化算法和模型的正则化。
2、矩阵模板:
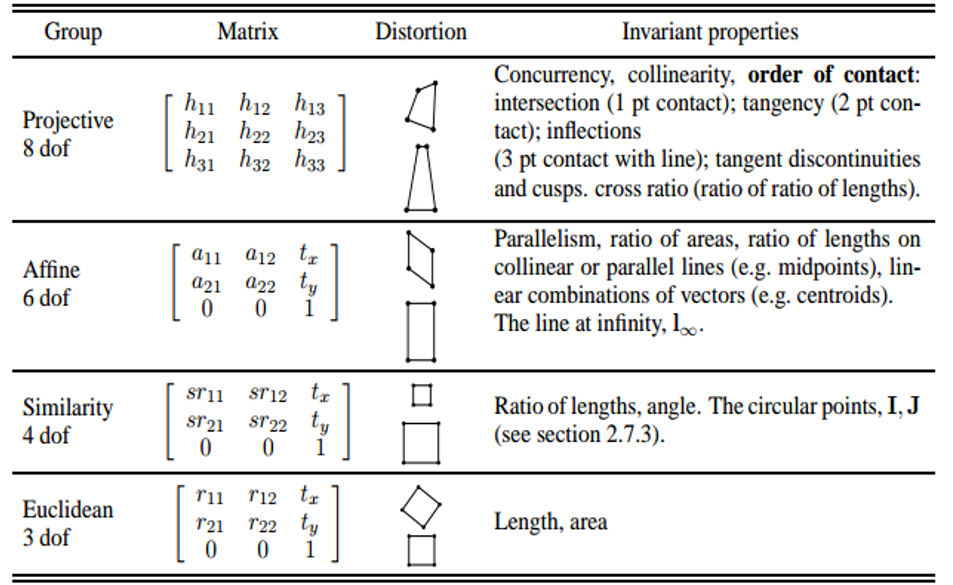
定义矩阵模板是计算机科学中的一种数据结构模板,用于表示和操作矩阵数据,在计算机编程中,矩阵模板通常用于实现矩阵的各种运算和操作,如加法、减法、乘法、转置等,矩阵模板可以支持多种数据类型,如整数、浮点数等,并提供了方便的接口供用户进行矩阵操作。
应用领域矩阵模板在计算机图形学、图像处理、数值计算等领域有广泛的应用,在线性代数库、机器学习库等软件开发中,矩阵模板也是常见的组成部分,用于实现高效的矩阵运算和算法优化。
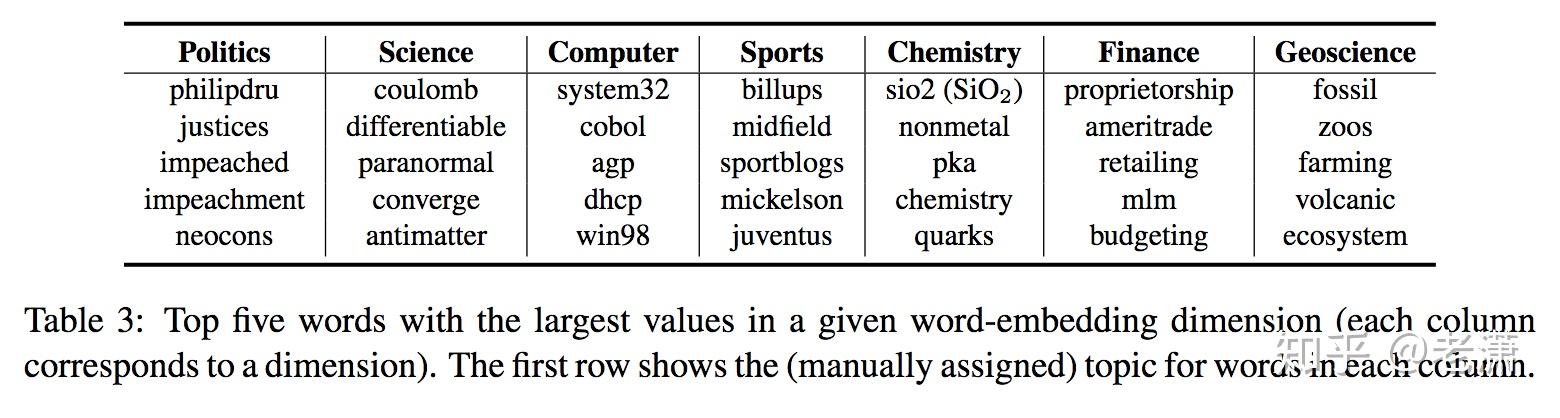
矩阵模和矩阵模板分别属于数学和计算机科学的范畴,矩阵模是用于衡量矩阵大小和性质的数学工具,而矩阵模板则是用于在计算机编程中表示和操作矩阵数据的数据结构模板,两者虽然名称相似,但在实际应用中有不同的作用和重要性。
 TIME
TIME
